【Python】set(セット)の使い方と集合演算を解説

この記事では、Pythonのset(セット)の使い方と集合演算について解説します。

setとは、順序を持たない複数の要素を格納することができるデータ型の一つです。最大の特徴としては重複した要素を格納できないことです。

また、セットは集合演算をサポートしています。集合演算は、セット同士の積集合、和集合、差集合などの操作を行うことができます。これにより、データの比較や重複の排除など、さまざまな処理を行うことが可能となっています。

それでは、setの使い方を見ていきましょう！

set(セット)とは？

setとは、順序を保持せず、重複する要素を持てないミュータブルなコレクションです。 ちなみに、異なる型の要素を格納することはできます。

リストやタプルなどに格納されている重複する要素を削除したい場合、一時的にセットに変換することでまとめて重複する要素を取り除くことができます。

また、setは「集合」とも呼ばれ、集合演算に用いられます。

イミュータブルなsetである「frozenset」も用意されています。

setの生成・初期化

空のsetを生成するにはset()を使います。

変数名 = set()

{}内に要素を,(カンマ)区切りで指定することで初期値を指定できます。

変数名 = {要素1, 要素2, ..., 要素N}

試しにsetを生成・出力してみます。

# setの生成
s = {1, 2, 3, 1, 2, 4}

print(s)
print(type(s))

実行結果

{1, 2, 3, 4}
<class 'set'>

空のセットを生成する際に{}を代入すると辞書として見なされてしまうので注意してください。

s = {}

print(s)
print(type(s))

実行結果

{}
<class 'dict'>

setの要素の取得

setは、シーケンスではない(順序を保持しない)ので[]を使ってインデックスを指定し、要素にアクセスすることができません。なので、要素を取得したい場合は、一時的にリストやタプルに変換するか、for文を使って要素を取得する必要があります。

# set初期化
s = {1, 2, 3}

# リストに型変換する
s_list = list(s)
print(s_list[0])

# for文を使う
for val in s:
    print(val)

ちなみに、[]を使ってインデックスでアクセスするとTypeErrorが送出される。

s = {1, 2, 3}
print(s[0])

実行結果

Traceback (most recent call last):
  File "/Users/user/Desktop/Python/test.py", line 2, in 
    print(s[0])
TypeError: 'set' object is not subscriptable

setに要素を追加する

setに要素を追加するには、以下のような方法があります。

任意の要素の追加[add]

add()メソッドを使って任意の要素を追加できます。もちろん、add()メソッドを使って要素を追加した場合でも重複する要素だったら削除されます。

set.add(追加する要素)

setに要素を追加して出力してみます。

vals = {1, 2, 3}

# 4を追加
vals.add(4)
print(vals)  # {1, 2, 3, 4}

# 重複している要素を追加してみる
vals.add(1)
print(vals)  # {1, 2, 3, 4}

複数の要素の追加[update]

update()メソッドの引数にリストやタプルなどを指定することで複数の要素を一度にまとめて追加することができます。

set.update(追加するコレクション)

試しに複数の要素を追加してみます。

vals = {1, 2, 3}
vals.update([1, 4, 'a'])

print(vals)  # {1, 2, 3, 4, 'a'}

setの要素を削除する

setの要素を削除するには、以下のような方法があります。

任意の要素の削除[remove] [discard]

remove()メソッド、またはdiscard()メソッドを使うことで引数で指定した要素を削除することができます。指定した要素がset内に存在しなかった場合、discard()メソッドはエラーを発生させませんが、remove()メソッドはKeyErrorを送出します。

set.remove(削除したい要素)
set.discard(削除したい要素)

試しにセットの要素を削除してみます。その中でdiscard()メソッドの引数に存在しない要素を指定してもエラーが起きないか試してみます。

vals = {1, 2, 3}

# 2を削除
vals.remove(2)

# 存在しない要素を指定
vals.discard(5)

print(vals)　 # {1, 3}

先頭の要素を取り出す[pop]

pop()メソッドを使うことで先頭の要素を取り出せます。

set.pop()

試しにpop()メソッドを使って先頭の要素を取り出してみます。

vals = {1, 2, 3}

val = vals.pop()
print(val)  # 1

val = vals.pop()
print(val)  # 2

val = vals.pop()
print(val)  # 3

print(vals) # set()

setが空のときに使うとKeyErrorが送出される。

vals = set()
vals.pop()

実行結果

Traceback (most recent call last):
  File "/Users/user/Desktop/Python/test.py", line 2, in 
    vals.pop()
KeyError: 'pop from an empty set'

全ての要素を削除する[clear]

clear()メソッド を使うことで全ての要素を削除することができます。

set.clear()

試しにセットの全ての要素を削除してみます。

vals = {1, 2, 3}
vals.clear()

print(vals)  # set()

長さの取得[len]

len()関数を使うことで長さを取得できます。

len(set)

setの長さを出力してみます。

vals = {1, 2, 3}

print(len(vals))  # 3

setの集合演算

setで集合演算する方法を紹介します。

和集合[union][|]

和集合を求めるには、union()メソッド、または｜演算子を使います。

set.union(配列)

set1 | set2

和集合とは「どちらか片方には存在する要素」を集めます。
図で表すと以下のようになります。

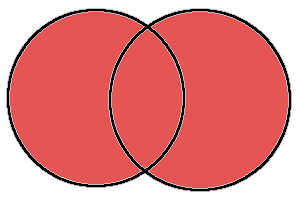
試しに和集合を計算してみましょう。

vals1 = {1, 2}
vals2 = {3, 4}

union = vals1.union(vals2)
print(union)  # {1, 2, 3, 4}

union = vals1 | vals2
print(union)  # {1, 2, 3, 4}

union()メソッドには、複数の配列を指定可能でリスト・タプルも指定できます。

vals1 = {1, 2}
vals2 = {3, 4}

union = vals1.union(vals2, [5, 6], (7, 8))
print(union)  # {1, 2, 3, 4, 5, 6, 7, 8}

積集合[intersection][&]

積集合を求めるには、intersection()メソッド、または&演算子を使います。

set.intersection(配列)

set1 & set2

積集合とは、「両方に入っている要素」を集めます。
図で表すと以下のようになります。

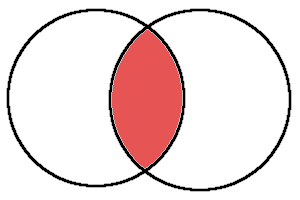
試しに積集合を計算してみましょう。

vals1 = {1, 2, 3}
vals2 = {2, 3, 4}

intersection = vals1.intersection(vals2)
print(intersection)  # {2, 3}

intersection = vals1 & vals2
print(intersection)  # {2, 3}

intersection()メソッドには複数の配列を指定可能でリスト・タプルも指定できます。

vals1 = {1, 2, 3, 4}
vals2 = {2, 3, 4, 5}

intersection = vals1.intersection(vals2, [3, 4, 5, 6], (4, 5, 6, 7))
print(intersection)  # {4}

差集合[difference][-]

差集合を求めるには、difference()メソッド、またはー演算子を使います。

set.difference(配列)

set1 - set2

差集合とは「ある集合から別の集合の要素を取り除いて残った要素」を集めます。
図で表すと以下のようになります。

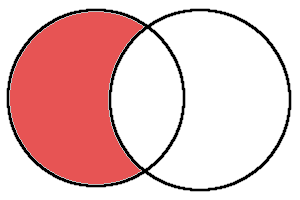
試しに差集合を計算してみましょう。

vals1 = {1, 2, 3}
vals2 = {2, 3, 4}

difference = vals1.difference(vals2)
print(difference)  # {1}

difference = vals1 - vals2
print(difference)  # {1}

difference()メソッドは、複数の配列を指定可能でリスト・タプルも指定できます。

vals = {1, 2, 3, 4, 5}

difference = vals.difference([2, 3], (4, 5))
print(difference)  # {1}

対称差集合[symmetric_difference][^]

対象差集合を求めるには、symmetric_difference()メソッド、または^演算子を使います。

set1.symmetric_difference(set2)

set1 ^ set2

対称差集合とは「どちらか片方のみに存在する要素」を集めます。
図で表すと以下のようになります。

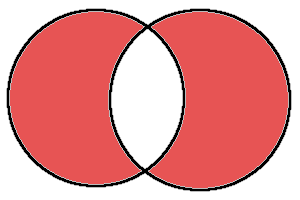
試しに対称差集合を計算してみましょう。

vals1 = {1, 2, 3}
vals2 = {2, 3, 4}

s_d = vals1.symmetric_difference(vals2)
print(s_d)  # {1, 4}

s_d = vals1 ^ vals2
print(s_d)  # {1, 4}

symmetric_difference()メソッドは、同時に複数の配列を指定できません。さらに、他のメソッドとは違いset同士でしか計算できません。

同時に複数の計算がしたい場合は演算子を使ってください。

vals1 = {1, 2, 3}
vals2 = {2, 3, 4}

s_d = vals1 ^ vals2 ^ {3, 4, 5}
print(s_d)  # {1, 3, 5}

まとめ

この記事では、Pythonのset(集合)の使い方を解説をしました。

setを使うことでコレクション内の重複している要素をまとめて削除できたり、集合演算することができました。集合演算にのみに使用したい場合は、frozensetを使うことでより効率良く行うことができます！

それでは今回の内容はここまでです。ではまたどこかで〜( ・∀・)ﾉ